Después de haber visto varios métodos de ordenamiento en clase de Algoritmos, mientras estaba ordenando un mazo de cartas para practicar, me surgió una duda. Así como hay algoritmos para ordenar cosas, ¿Qué pasa si lo que quiero ahora es mezclar el mazo de cartas?
Debería ser más fácil que ordenarlo, ¿No? Al menos no tengo que seguir un orden específico, podría hacer lo que quiera, pero ¿Cómo?.
Una forma que se nos puede ocurrir es asignar un número al azar a cada carta, y después ordenarlas según esos números. Por supuesto hay otras formas mas eficientes de mezclar un mazo de cartas, pero en todas entran en juego números elegidos al azar, o números aleatorios.
Pero, ¿Cómo hago para elegir número al azar? ¿Existe algún algoritmo que pueda generar números realmente aleatorios?.
Obviamente que si buscamos en Google “Generar números al azar en <tu lenguaje de programación favorito aquí>” seguramente encontraremos métodos del lenguaje tipo Math.random() que hacen justamente eso, pero la gracia, igual que con los métodos de ordenamiento, es conocer y entender cómo funcionan esos algoritmos por dentro.
Los números aleatorios
Entonces, empecemos por lo básico, queremos saber cómo generar números aleatorios, pero ¿Qué es un número aleatorio? Por ejemplo, ¿Es 7 un número aleatorio?
Bueno, no podemos decir nada al respecto, pero si le preguntaríamos a Knuth nos diría que:
En realidad nunca hablamos de si un número particular es aleatorio, si no de una secuencia de números aleatorios independientes, con una distribución particular. Esto significa (mas o menos) que cada número fué obtenido al azar, sin tener ninguna relación con los otros números de la secuencia, y que cada número tiene una probabilidad específica de pertenecer a un rango dado de valores.
Para entenderlo mejor, podemos dividir esto en dos afirmaciones:
- Los números son obtenidos al azar en forma independiente.
- Los números tienen una distribución particular, esto es, cada número tiene una probabilidad específica de pertenecer a un rango dado de valores.
La primera afirmación nos dice que, por ejemplo, si nos dan los primeros 1000 números de una secuencia aleatoria, como cada número es obtenido de forma independiente de los demás, nos sería imposible calcular o adivinar de forma precisa cuál va a ser el siguiente número de la secuencia (solamente podríamos acertar de suerte).
La segunda nos dice que los números de la secuencia responden a una distribución particular. Por ejemplo, si la distribución es como la siguiente:
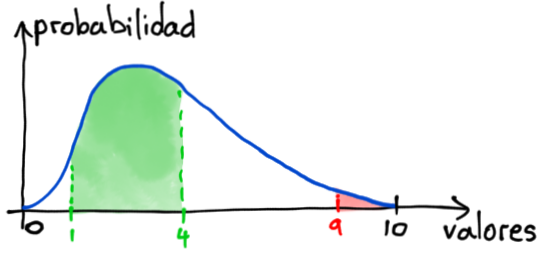
Vemos que es más probable obtener números entre 1 y 4 que entre 9 y 10. De todos modos, los valores de la secuencia siguien siendo aleatorios, solo que la probabilidad de encontrar números entre 1 y 4 en la secuencia es mayor que la probabilidad de encontrar números entre 9 y 10.
Sin embargo, usualmente, cuando nos referimos a números aleatorios estamos pensando en que tenemos la misma probabilidad de obtener cualquier número, como cuando lanzamos un dado (que tenemos la misma probabilidad de obtener cualquier número del 1 al 6). Entonces, la distribución podría ser como la siguiente:
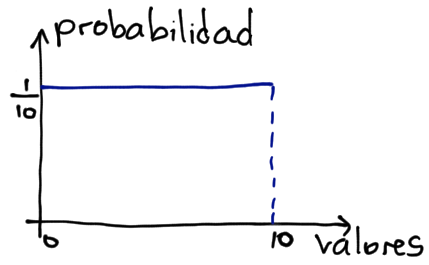
Este tipo de distribución se denomina distribución uniforme, y se denota como $U(\text{min}, \text{max})$, donde $\text{min}$ y $\text{max}$ representan el valor máximo y mínimo que podemos obtener. En el ejemplo, la distribución sería $U(0, 10)$.
En el caso de que los números sólo puedan tomar valores enteros entre 1 y 6 (como cuando lanzamos un dado, que no nos puede salir un 4,17), entonces tenemos una distribución uniforme discreta:
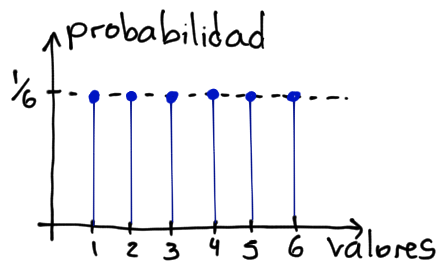
Ahora, que cualquiera de los 6 números tenga la misma probabilidad de ser el siguiente en la secuencia no quiere decir que no pueda existir una secuencia obtenida al azar en donde aparezca 100 veces seguidas el número 4, por ejemplo, por más que esto sea muy poco probable.
Además, como los números son independientes, si en la secuencia va apareciendo 99 veces seguidas el número 4, la probabilidad de que salga una vez más a continuación sigue siendo 1/6.
Bueno, ya tenemos entonces una mejor idea sobre qué son los números aleatorios. En el siguiente post vamos a empezar a pensar de qué maneras podríamos intentar generarlos.
Referencias
- Donald E. Knuth (1997) The Art of Computer Programming, Volume 2: Seminumerical Algorithms (3ra edición).
